The significance of the CO2 lag
Posted on 18 May 2010 by John Cook
When we examine past climate change using ice cores, we observe that CO2 lags temperature. In other words, a change in temperature causes changes in atmospheric CO2. This is due to various processes such as warmer temperatures causing the oceans to release CO2. This has lead some to argue that the CO2 lag disproves the warming effect of CO2. However, this line of thinking doesn't take in the full body of evidence. We have many lines of empirical evidence that CO2 traps heat. Decades of lab experiments reveal how CO2 absorbs and scatters infrared radiation. Satellite measurements find CO2 trapping heat and surface measurements confirm more radiation at CO2 wavelengths returning to the Earth's surface. So the full body of evidence gives us these two facts: warming causes more CO2 and more CO2 causes warming. The significance should by now be obvious. The CO2 lag is evidence of a climate positive feedback.
The magnitude of this positive feedback is calculated in Positive feedback between global warming and atmospheric CO2 concentration inferred from past climate change (Scheffer 2006). In this paper, they use reconstructions of past CO2 and temperature to empirically calculate the positive feedback between global warming and CO2. First, they look at pre-industrial CO2 variations during glacial cycles and the Little Ice Age. The relationship between CO2 and temperature is roughly linear.
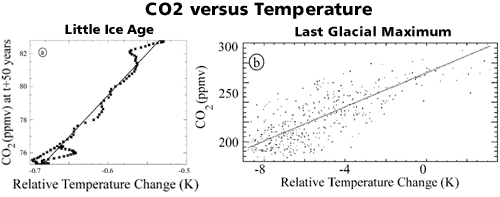
Figure 1. Relationships between past atmospheric CO2 concentrations and reconstructed temperatures. (a) Reconstructed Northern Hemisphere temperatures of the period 1500-1600 plotted against CO2 levels 50 years later from the Law Dome record. (b) CO2 vs temperature for a 400.000 years period of glacial cycles reconstructed from the Vostok ice core.
Over these periods, changes in CO2 are assumed to be primarily driven by temperature. This is because mechanisms other than changing CO2 (such as changes in solar output) drove temperature over these periods. So looking at Figure 1, we can calculate the effect that temperature change has on CO2 levels. However, this is complicated by the fact that different carbon cycle processes operate on different time scales. On a time scale of years, warming has an effect of around 3 ppm of CO2 per degree Celsius. On a scale of centuries, the effect is much larger - around 20 ppm of CO2 per degree Celsius.
What we're interested in is the expected global warming by the end of the 21st century so century time-scales are the focus. The most important period for estimating sensitivity of CO2 to temperature on century time-scales is the Little Ice Age. Figure 1a shows how CO2 levels dropped (with a time lag of 50 years) in response to the drop in temperature in this period. From this is calculated a positive feedback of between 15 to 78% on a century-scale.
The benefit of this study is it provides an independent, empirical method of calculating the positive feedback from the CO2 lag. These results are consistent with what's been found in simulation studies. So when someone mentions to you that CO2 lags temperature, remind them they're actually invoking evidence for a positive feedback that further increases global warming by an extra 15 to 78%.































 Arguments
Arguments























 0
0  0
0






Comments