Arctic sea ice melt - natural or man-made?
Posted on 9 June 2008 by John Cook
Arctic sea ice has declined steadily since the 1970s. However, the 2007 summer saw a dramatic drop in sea ice extent, smashing the previous record minimum set in 2005 by 20%. This has been widely cited as proof of global warming. However, a popular mantra by climatologists is not to read too much into short term fluctuations - climate change is more concerned with long term trends. So how much of Arctic melt is due to natural variability and how much was a result of global warming?
The long term trend in Arctic sea ice
Global warming affects Arctic sea ice in various ways. Warming air temperatures have been observed over the past 3 decades by drifting buoys and radiometer satellites (Rigor 2000, Comiso 2003). Downward longwave radiation has increased, as expected when air temperature, water vapor and cloudiness increases (Francis 2006). More ocean heat is being transported into Arctic waters (Shimada 2006).
As sea ice melts, positive feedbacks enhance the rate of sea ice loss. Positive ice-albedo feedback has become a dominant factor since the mid-to-late 1990s (Perovich 2007). Older perennial ice is thicker and more likely to survive the summer melt season. It reflects more sunlight and transmits less solar radiation to the ocean. Satellite measurements have found over the past 3 decades, the amount of perennial sea ice has been steadily declining (Nghiem 2007). Consequently, the mean thickness of ice over the Arctic Ocean has thinned from 2.6 meters in March 1987 to 2.0 meters in 2007 (Stroeve 2008).
Global warming has a clearly observed, long term effect on Arctic sea ice. In fact, although climate models predict that Arctic sea ice will decline in response to greenhouse gas increases, the current pace of retreat at the end of the melt season is exceeding the models’ forecasts by around a factor of 3 (Stroeve 2007).
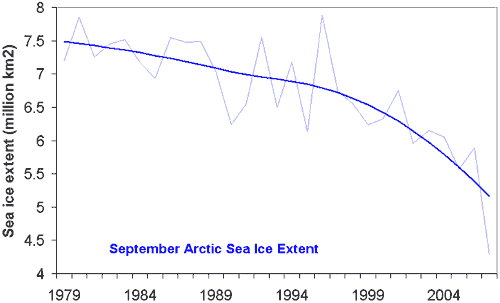
Figure 1: September Arctic Sea Ice Extent (thin, light blue) with long term trend (thick, dark blue). Sea ice extent is defined as the surface area enclosed by the sea ice edge (where sea ice concentration falls below 15%).
What caused the dramatic ice loss in 2007?
The sudden drop in sea ice extent in 2007 exceeded most expectations. The summer sea ice extent was 40% below 1980's levels and 20% below the previous record minimum set in 2005. The major factor in the 2007 melt was anomalous weather conditions.
An anticyclonic pattern formed in early June 2007 over the central Arctic Ocean, persisting for 3 months (Gascard 2008). This was coupled with low pressures over central and western Siberia. Persistent southerly winds between the high and low pressure centers gave rise to warmer air temperatures north of Siberia that promoted melt. The wind also transported ice away from the Siberian coast.
In addition, skies under the anticyclone were predominantly clear. The reduced cloudiness meant more than usual sunlight reached the sea ice, fostering strong sea ice melt (Kay 2008).
Both the wind patterns and reduced cloudliness were anomalies but not unprecedented. Similar patterns occurred in 1987 and 1977. However, past occurances didn't have the same dramatic effect as in 2007. The reason for the severe ice loss in 2007 was because the ice pack had suffered two decades of thinning and area reduction, making the sea ice more vulnerable to current weather conditions (Nghiem 2007).
Conclusion
Recent discussion about ocean cycles have focused on how internal variability can slow down global warming. The 2007 Arctic melt is a sobering example of the impact when internal variability enhances the long term global warming trend.































 Arguments
Arguments























 0
0  0
0






Comments