Empirical evidence that humans are causing global warming
What the science says...
| Select a level... |
 Basic
Basic
|
 Intermediate
Intermediate
| |||
|
Less energy is escaping to space: Carbon dioxide (CO2) acts like a blanket; adding more CO2 makes the 'blanket' thicker, and humans are adding more CO2 all the time. |
|||||
Climate Myth...
There's no empirical evidence
"There is no actual evidence that carbon dioxide emissions are causing global warming. Note that computer models are just concatenations of calculations you could do on a hand-held calculator, so they are theoretical and cannot be part of any evidence." (David Evans)
At a glance
Empirical evidence? None? That's a big bold statement to make, so let's take a look. 'Empirical' is defined as something that may be actually measured and presented as a finding. Let's treat the topic as a criminal prosecution. The accused is CO2 and the accusation is that its increased levels through our emissions are warming the planet. As with all court cases, it's important to present an accurate account of events. So firstly, we'll examine the background to this particular case.
It all started in the 1820s, when French physicist Joseph Fourier had worked out that, at its distance from the Sun, Earth should be very cold. He proposed that Earth's atmosphere must contain something that kept the planet warm, like some invisible blanket. His ideas were, it turned out, correct albeit incomplete.
Some decades passed before the nature of Fourier's blanket was discovered. This was done through a series of experiments involving various gases. Interestingly, two investigators worked on it independently, John Tyndall, in the UK and Eunice Foote in the USA. Impressively, their results were virtually identical.
Foote, writing in 1856, was the first scientist to state that carbon dioxide can trap energy. She predicted that if there had been more CO2 in the atmosphere at times past, an increased temperature would have prevailed. That was something the geologists already knew. Tyndall went on to write, in 1861, that on top of carbon dioxide, hydrocarbons - such as methane - would have even greater effects at very low concentrations. The greenhouse effect and its key players had been identified.
The landmark paper, "The Carbon Dioxide Theory of Climatic Change", was published just under a hundred years later. Essentially, it stated what we know now. Without the atmosphere and its greenhouse gases, Earth would be an uninhabitable iceball. As Fourier started to reason all that time ago, greenhouse gases act like a blanket. They keep Earth warm by inhibiting the escape of energy back into space. Humans are adding CO2 to the atmosphere, mainly by burning fossil fuels, thereby intensifying the effect.
That's the background. As we emit more greenhouse gases, the effect is like wrapping yourself in a thicker blanket. Even less heat is lost. So how can we tell that? How can we find hard evidence, like good CCTV footage of our suspect up to their mischief?
How about measuring it?
Satellites orbiting our planet carry sensitive instruments on board. Through them we can measure how much energy is arriving from the Sun. We can measure how much energy is leaving the Earth, out into space. So right there we have two things to compare.
What do the measurements tell us? Over the last few decades since satellites became available, there has been a gradual decrease in the energy heading from Earth's surface back into space. Yet in the same period, the amount of energy arriving from the Sun has hardly changed at all. Something is hanging onto that energy and that something is getting stronger. That something is carbon dioxide - doing exactly as Foote and Tyndall said it would 160 plus years ago.
Verdict: guilty on all counts.
Please use this form to provide feedback about this new "At a glance" section. Read a more technical version below or dig deeper via the tabs above!
Further details
The well-established theory that man-made CO2 is causing global warming is supported as well as any chain of evidence in a rock-solid court case. CO2 keeps the Earth warmer than it would be without it. It has done so for most of geological time. Humans are adding substantial amounts of CO2 to the atmosphere, mainly by burning fossil fuels. Empirical evidence abounds to support the contention that the rising temperatures are being caused by that increasing CO2.
The Earth is wrapped in an invisible blanket
It is the Earth’s atmosphere that makes most life possible. To understand this, we can look at the moon. On the surface, the moon’s temperature during daytime can reach 100°C (212°F). At night, it can plunge to minus 173°C, or -279.4°F. In comparison, the coldest temperature on Earth was recorded in Antarctica: −89.2°C (−128.6°F). According to the WMO, the hottest was 56.7°C (134°F), measured on 10 July 1913 at Greenland Ranch (Death Valley).
Man could not survive in the temperatures on the moon, even if there was air to breathe. Humans, plants and animals can’t tolerate the extremes of temperature on Earth unless they evolve special ways to deal with the heat or the cold. Nearly all life on Earth lives in areas that are more hospitable, where temperatures are far less extreme.
Yet the Earth and the moon are virtually the same distance from the sun, so why do we experience much less heat and cold than the moon? The answer is because of our atmosphere. The moon doesn’t have one, so it is exposed to the full strength of energy coming from the sun. At night, temperatures plunge because there is no atmosphere to keep the heat in, as there is on Earth.
Without the atmospheric greenhouse effect, Earth would be approximately 33°C (59.4°F) cooler than it actually is. That would make most of the surface uninhabitable for humans. Agriculture as we know it would be more or less impossible if the average temperature was −18 °C.
Greenhouse gases act like a blanket, keeping the Earth warm by preventing some of the sun’s energy being re-radiated from Earth's warmed surface, back out into space. If we add more greenhouse gases to the atmosphere, the effect is like wrapping yourself in a thicker blanket: even less heat is lost. So how can we tell what effect CO2 is having on temperatures, and if the increase in atmospheric CO2 is really making the planet warmer?
The heat-trapping effects of CO2 and other greenhouse gases were discovered in the mid-19th century but we can do more sophisticated stuff these days. We can measure the heat energy going into Earth's climate system and that coming back out.
In 1970, NASA launched the IRIS satellite measuring infrared spectra. In 1996, the Japanese Space Agency launched the IMG satellite which recorded similar observations. Both sets of data were compared to discern any changes in outgoing radiation over the 26 year period (Harries et al. 2001). What they consistently found was a drop in outgoing radiation.
This change in outgoing radiation was consistent with theoretical expectations. Thus the Harries paper found "direct experimental evidence for a significant increase in the Earth's greenhouse effect". This result has been confirmed by subsequent papers using data from later satellites (Griggs & Harries 2004, Chen et al. 2007). In the same period, the amount of energy arriving from the sun has hardly changed at all.
When there is more energy coming in from the Sun than there is escaping back out to space, it should come as no surprise to learn that our climate is accumulating heat. The planet's total heat build up can be derived by adding up the heat content from the ocean, atmosphere, land and ice (Murphy et al. 2009). Just since 1998, the planet has accumulated heat energy equivalent to the yield of 3,260,000,000 Hiroshima-sized atomic bombs.
The primary greenhouse gases responsible for the trapping of heat – carbon dioxide (CO2), methane (CH4), water vapour, nitrous oxide and ozone – comprise around 1% of the air. The main components of the atmosphere – nitrogen and oxygen – are not greenhouse gases, because they are virtually transparent to long-wave or infrared radiation.
For our next piece of evidence, we must look at the amount of CO2 in the air. We know from bubbles of air trapped in ice cores that before the industrial revolution the amount of CO2 in the air was approximately 280 parts per million (ppm). In June 2013, the NOAA Earth System Research Laboratory in Hawaii announced that, for the first time in millions of years, the amount of CO2 in the air had gone above 400 ppm. It's now getting on for 420 ppm. That information gives us the next piece of evidence; CO2 has increased by 50% in the last 150 years.
The Smoking Gun
The final piece of evidence is ‘the smoking gun’, the proof that CO2 is causing the increase in temperature. CO2 traps energy at very specific wavelengths, while other greenhouse gases trap different wavelengths. In physics, these wavelengths can be measured using a technique called spectroscopy. Here’s an example:
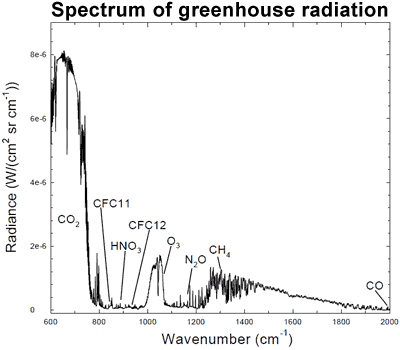
Fig. 1. Spectrum of the greenhouse radiation measured at the surface. Greenhouse effect from water vapour is filtered out, showing the contributions of other greenhouse gases (Evans et al. 2006).
The graph shows different wavelengths of energy, measured at the Earth’s surface. Among the spikes you can see energy being radiated back to Earth by ozone (O3), methane (CH4), and nitrous oxide (N20). But the spike for CO2 on the left dwarfs all the other greenhouse gases, and tells us something very important: most of the energy being trapped in the atmosphere corresponds exactly to the wavelength of energy captured by CO2.
Summing Up
Like a detective story, first you need a victim, in this case the planet Earth: more energy is remaining in the atmosphere.
Then you need a method, and ask how the energy could be made to remain. For that, you need a demonstrable mechanism by which energy can be trapped in the atmosphere, and greenhouse gases provide that mechanism.
Next, you need a ‘motive’. Why has this happened? Because CO2 has increased by nearly 50% in the last 150 years and the increase is mostly from burning fossil fuels.
And finally, the smoking gun, the evidence that proves ‘whodunit’: energy being trapped in the atmosphere corresponds exactly to the wavelengths of energy captured by CO2.
The last point is what places CO2 at the scene of the crime. The investigation by science builds up empirical evidence that proves, step by step, that man-made carbon dioxide is causing the Earth to warm up.
Finally, the myth-creator refers to climate models as "concatenations of calculations you could do on a hand-held calculator". That statement demonstrates nothing more than a limited grasp of what models are and do and is rebutted at this post in our series.
Last updated on 9 July 2023 by John Mason. View Archives































 Arguments
Arguments




































I wish that were true. I list a selection of skeptic articles arguing that human contribution to atmospheric CO2 is tiny and that increasing CO2 doesn't cause much warming. Ian Plimer who I'm sure considers himself a serious skeptic argues both points in his book Heaven and Earth.
You do make a good point though. I thought ending this article with 'the planet is accumulating heat' was sufficient to show humans are causing global warming. However, I think an extra step is now required, something to the effect of 'extra heat causes surface warming' (I'll work on a less clumsily worded version). In other words, that our climate is sensitive to radiative forcings. I would base this not on models but on the many papers looking at empirical data of temperature change versus forcings to calculate climate sensitivity.
Re ocean heat, note that the Bob Tisdale webpage you link to looks at upper ocean heat from 0 to 700 metres deep. Upper ocean heat shows more variability than ocean heat calculated to greater depths as the upper ocean exchanges heat with deeper waters. Ocean heat content calculated to 2000 metres deep finds less variability and that oceans are still accumulating heat (von Schuckmann 2009). Note - this analysis is based solely on Argo data, hence the 2003 to 2008 time frame: