Posted on 13 August 2011 by Doug Mackie

This post is number 15 in a series about ocean acidification. Other posts: Introduction, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.

Welcome to the 15^th post in our series about ocean acidification. Some more background theory in this post including a walk through a calculation that troubles many students. And if it all reads like high school chemistry that is because it is. The fundamentals of ocean acidification are that simple.

Solubility expressions (post 3) are written and calculated in terms of the simplest equation for the reaction. In the case of calcium carbonate this equation is:

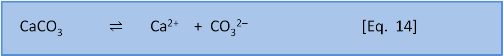
Equation 14 is the baseline dissolution of calcium carbonate. (If we consider external influences like the weathering of limestone by rain containing carbonic acid then the dissolution also involves the release of bicarbonate HCO₃^– and consumption of CO₂).

Back in post 3 we wrote of doing calculations about dissolution or precipitation in comparison to solubility. But, as we now know, the dissolution reaction depends on the concentration of both parts of an ionic salt (e.g. the Ca²⁺ and the CO₃^2–). For this reason solubility varies, depending on the concentration of ions in the solvent. So chemists prefer to use an expression that is derived from the equilibrium constant.

We might think that we could write an equilibrium constant for the reaction in Eq. 14 as:

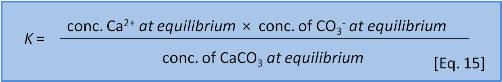
But Eq. 15 is wrong. Dissolutions are heterogeneous. That is, they involve different phases or states of matter (e.g. solid, liquid, gas). Because the CaCO₃ is a solid it doesn't have a dissolved concentration in water. So we leave it out and instead write an expression called a solubility product or K_sp as:

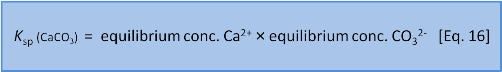
In this series we have done our best to avoid jargon and too much symbolic representation but now we think it will help if we say that chemists write concentration expressions using square brackets and (often but with some variance) use a subscript e to mean the concentration at equilibrium so we now have:

The solubility product is exactly what we need to decide whether or not something will precipitate or dissolve. Very often this is all the answer that is required. But it is also possible to use the solubility product to derive the solubility, s, which tells us how much of a substance dissolves.

For a simple substance like CaCO₃ this is easy. We imagine placing a lump of CaCO₃ in pure water (*) and waiting until the system has reached equilibrium. Though, as we have noted several times, just because a reaction is thermodynamically favoured does not mean it will happen quickly.

(*In the real world it makes a huge difference if we are talking about water that is in contact with atmospheric CO₂ or not and whether or not the water remains or becomes in contact with the atmosphere.)

Thus, to dissolve the CaCO₃ we could add powdered limestone to a known volume of water in a beaker and stir until it had dissolved. Finally we would reach a point where the limestone would no longer dissolve no matter how much stirring and would start to pile up on the bottom of the beaker. (One of us has a friend who comes close to achieving this with sugar in their coffee). When as much CaCO₃ has dissolved as is ever going to, we imagine measuring the concentration of Ca²⁺ dissolved in what is now a solution of Ca²⁺ and CO₃^2–. We call this value the solubility, s. Since CaCO₃ contains 1 Ca²⁺ for each CO₃^2– we asssume that the concentration of CO₃^2– is also s. Thus we can say that:

As we should expect, the calcium carbonate polymorphs calcite and aragonite have different solubility products. We will get to seawater in a moment but in a simple freshwater system at 25^oC (see caveats in the next post) K_sp (calcite) = 4.5 ×10^–9 and K_sp (aragonite) = 6.0 ×10^–9 (the units here, mol² L^–2, are not vital for our purposes and as they can be confusing we won't use them). We can calculate that in freshwater the solubility of calcite = (4.5 ×10^–9)^1/2 ≈ 7 ×10^–5 mol L^–1 and for aragonite ≈ 8×10^–5 mol L^–1. Note 1: x^1/2 is another way of writing √x, the square root of x. Note 2:  We have been a little sloppy in these posts about concentration units. The volume of water changes a function of temperature (and pressure) so it is actually better practice to use mass (kg) instead of volume (L) but most laypeople are more used to seeing concentration as a mass per volume so we have mostly used mol L^-1).

The assumption that the concentrations of Ca²⁺ and CO₃^2– are equal is valid if the only source of each ion is the dissolution process; that is if CaCO₃ is the only source of both Ca²⁺ and CO₃^2–. But what happens when there is another supply source for one of the ions? This is called the common ion effect. You may remember this from high school chemistry but if not here is a quick refresher.

Imagine, for example, that our beaker of water already had some calcium chloride dissolved into it and that we are adding calcite. That is, it contains a solution of Ca²⁺ and Cl^–. Let's say that the concentration of Ca²⁺ already in the beaker before we begin to try dissolving any calcite is 1 ×10^–3 mol L^–1. The solution in the beaker and the calcite have calcium ions in common.

When the calcite dissolves it produces both Ca²⁺ and CO₃^2– and the concentration of both ions increases by s, the solubility of calcite. So can we use Eq. 17? Not yet; recall that the concentration of calcium was already 1 ×10^–3 while the concentration of carbonate was initially zero).   The easiest way to visualise the system is to set up a concentration table to describe the system before, during and after the addition of the calcite.

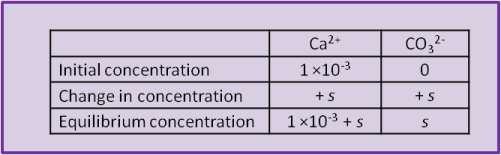
Using the equilibrium values we can calculate a numerical value for s:

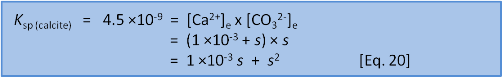
We can solve for s in two ways. First, we can rearrange and solve as a quadratic:

Or, if it has been a long time since high school  maths and you don't remember if the quadratic equation uses 4ac or 4AD then we can take a shortcut. We know that s = 7 ×10^–5 when we do this in freshwater without the extra calcium present before we start. So we have a pretty fair idea that the new s will be of a similar order of magnitude. We can see that the initial concentration of calcium, 1 ×10^–3, is very much bigger than 7 ×10^–5. This lets us make the assumption that 1 ×10^–3 + s ≈ 1 ×10^–3. In this case we have:

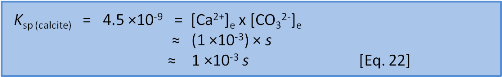
This shortcut answer is less than 1% different from the quadratic solution and there is something of an art in knowing when you can get away with it and when the full solution is needed. Both answers show that if some calcium (1 × 10-3 mol L-1) is already present then the solubility of calcite changes by about a factor of 15 from 7 ×10^–5 to 4.5×10^–6 mol L^-1. Similar calculations help us predict what will happen when the concentration of one of the ions, say carbonate, has been removed by an external factor.

These sorts of interactions (and some other complex interactions that await you if you take a university chemistry course) explain why seawater chemistry is so very different to freshwater chemistry. In surface seawater at 25^oC and 35 salinity the K_sp (calcite) = 4.4 ×10^–7 and K_sp (aragonite) = 6.5 ×10^–7. We can now calculate that the solubilities are 6.6 ×10^-4 and 8.1 ×10^-4 molL^-1, respectively. That is, both calcium carbonate polymorphs are about 10 times more soluble in seawater than in freshwater. Next post: Saturation and when K_sp changes.

Written by Doug Mackie, Christina McGraw, and Keith Hunter  This post is number 15 in a series about ocean acidification. Other posts: Introduction, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, Summary 1 of 2, Summary 2 of 2.