Monckton Myth #3: Linear Warming
Posted on 18 January 2011 by dana1981
 In his recent response to Steketee's article in The Australian, Monckton's argument #5 reads as follows:
In his recent response to Steketee's article in The Australian, Monckton's argument #5 reads as follows:
In the 40 years since 1970, global temperatures have risen at a linear rate equivalent to around 1.3 °C/century. CO2 concentration is rising in a straight line at just 2 ppmv/year at present and, even if it were to accelerate to an exponential rate of increase, the corresponding temperature increase would be expected to rise merely in a straight line. On any view, 1.3 °C of further “global warming” this century would be harmless. The IPCC is predicting 3.4 °C, but since the turn of the millennium on 1 January 2001 global temperature has risen (taking the average of the two satellite datasets) at a rate equivalent to just 0.6 °C/century, rather less than the warming rate of the entire 20th century. In these numbers, there is nothing whatever to worry about – except the tendency of some journalists to conceal them.
This paragraph contains a number of erroneous statements. Firstly, according to both GISTEMP and HADCRUT3 (satellite data only began in 1979), the global temperature trend since 1970 is 1.6–1.7°C per century. Secondly, the atmospheric CO2 concentration has been accelerating (not linear). The rate of increase in atmospheric CO2 in the 2000's (2.2 parts per million by volume [ppmv] per year) was in fact 47% faster than the rate of increase in the 1990s (1.5 ppmv per year). Monckton uses these incorrect assertions to create the support for his incorrect argument - that if we continue with business-as-usual, global temperatures over the next century will increase at a constant, linear rate (or slower).
Temperature Response to CO2
Monckton claims that an exponential increase in atmospheric CO2 concentration would result in a linear increase in global temperature. But of course that depends on what the exponent is in the exponential increase. Monckton is referring to the logarithmic relationship between radiative forcing (which is directly proportional to the change in surface temperature at equilibrium) and the atmospheric CO2 increase. Note that we are not currently at equilibrium as there is a planetary energy imbalance, and thus further warming 'in the pipeline' from the carbon we've already emitted. Therefore, estimates of the rate of warming due to CO2 thus far will will be underestimates, unless accounting for this 'warming in the pipeline' (which Monckton does not).
This logarithmic relationship means that each doubling of atmospheric CO2 will cause the same amount of warming at the Earth's surface. Thus if it takes as long to increase atmospheric CO2 from 560 to 1120 ppmv as it did to rise from 280 to 560 ppmv, for example, then the associated warming at the Earth's surface will be roughly linear. So the question then becomes, how fast do we expect atmospheric CO2 to rise over the next century?
How Fast will Atmospheric CO2 Rise?
The IPCC addressed this question by examining a number of different anthropogenic emissions scenarios. Scenario A1F1 assumes high global economic growth and continued heavy reliance on fossil fuels for the remainder of the century. Scenario B1 assumes a major move away from fossil fuels toward alternative and renewable energy as the century progresses. Scenario A2 is a middling scenario, with less even economic growth and some adoption of alternative and renewable energy sources as the century unfolds. The projected atmospheric CO2 levels for these scenarios is shown in Figure 1.
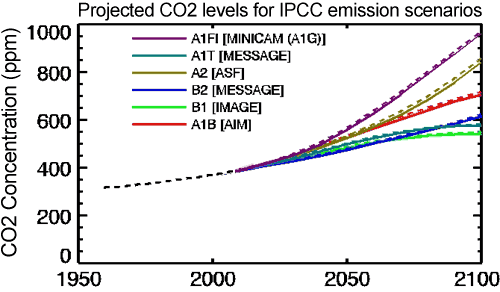
Figure 1: Atmospheric CO2 concentrations as observed at Mauna Loa from 1958 to 2008 (black dashed line) and projected under the 6 IPCC emission scenarios (solid coloured lines). (IPCC Data Distribution Centre)
In short, following the 'business as usual' approach which Monckton argues for, without major steps to move away from fossil fuels and limit greenhouse gas emissions, we will likely reach 850 to 950 ppmv of atmospheric CO2 by the year 2100. It will have taken approximately 200 years (from 1850 to 2050) for the first doubling of atmospheric CO2 from 280 to 560 ppmv, but it will only take another 70 years or so to double the levels again to 1120 ppmv. This will result in an accelerating rate of global warming, not a linear rate. Under Scenarios A2 and A1F1, the IPCC report projects that the global temperature in 2095 will be 2.0–6.4°C above 1990 levels (2.6-7.0°C above pre-industrial), with a best estimate of 3.4 and 4.0°C warmer (4.0 and 4.6°C above pre-industrial average surface temperatures), respectively.
Figure 2: Global surface temperature projections for IPCC Scenarios. Shading denotes the ±1 standard deviation range of individual model annual averages. The orange line is constant CO2 concentrations at year 2000 values. The grey bars at right indicate the best estimate (solid line within each bar) and the likely range. (Source: IPCC).
Life in the Fast Lane
Monckton claims that these projected amounts of warming have not been borne out in the surface temperature changes over the past decade. But there are many factors which impact short-term global temperatures, which may conceal the long-term warming caused by increasing atmospheric CO2. So if we want to know if the IPCC projections are realistic, rather than examining noisy short-term temperature data, we should examine how much atmospheric CO2 is increasing.
When we look at this data, we find that observed CO2 emissions in recent years have actually been tracking close to or above the worst case (A1F1) scenario.
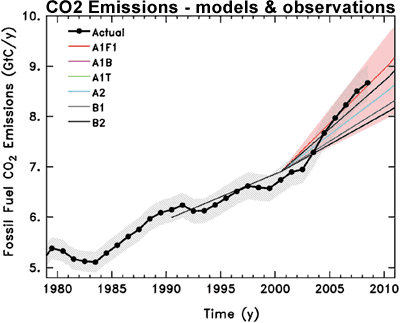
Figure 3: Observed global CO2 emissions from fossil fuel burning and cement production compared with IPCC emissions scenarios. The coloured area covers all scenarios used to project climate change by the IPCC (Copenhagen Diagnosis).
What Lies Ahead
So if we continue in a business-as-usual scenario, we should expect to see atmospheric CO2 levels accelerate rapidly enough to more than offset the logarithmic relationship with temperature, and cause the surface temperature warming to accelerate as well. Monckton's claim of a "straight line" increase in global temperature ignores that in his preferred 'business as usual' scenario, we are currently on pace to double the current atmospheric CO2 concentration (390 to 780 ppmv) within the next 60 to 80 years, and we have not yet even come close to doubling the pre-industrial concentration (280 ppmv) in the past 150 years. Thus the exponential increase in CO2 will outpace its logarithmic relationship with surface temperature, causing global warming to accelerate unless we take serious steps to reduce greenhouse gas emissions. In fact, to continue the current rate of warming over the 21st Century, we would need to achieve IPCC scenario B1 - a major move away from fossil fuels toward alternative and renewable energy.
As for what amount of global warming is "harmless" and "dangerous" we will examine this question later on in another upcoming Monckton Myth.































 Arguments
Arguments























 0
0  0
0 Yup, no problem.
Yup, no problem. --- from comment here.
Those temperature anomaly curves increase in slope regardless of the sensitivity used (those shown are 0.6, 1.7 and 3 degrees C per doubling of CO2). So your attempt to minimize the impact of increasing atmospheric CO2 is utterly incorrect; as jhudsy says, the gloomy predictions are indeed fully justified.
--- from comment here.
Those temperature anomaly curves increase in slope regardless of the sensitivity used (those shown are 0.6, 1.7 and 3 degrees C per doubling of CO2). So your attempt to minimize the impact of increasing atmospheric CO2 is utterly incorrect; as jhudsy says, the gloomy predictions are indeed fully justified.







Comments